GeNIe – aplikacja tworzenia grafów sieci bayesowskiej
Program modelowania GeNIe: https://download.bayesfusion.com/downloads/Academia/GeNIe/genie-academic-setup-3.0.6128-x86.exe
Manual programu GeNIe: https://support.bayesfusion.com/docs/GeNIe.pdf
Instalacja
Po ściągnięciu wersji instalacyjnej należy ją zainstalować na komputerze, w trakcie instalacji system Windows może zgłosić błąd zabezpieczeń przez Smart Filter podobny do poniższego obrazu.

Wynika to z tego, że kod instalatora nie został podpisany certyfikatem akceptowanym przez Microsoft. Tym niemniej możemy kliknąć na link More info i wybrać opcję, że chcemy pomimo tego uruchomić tę aplikację. Po uruchomieniu instalatora zgadzamy się (albo i nie 😉 ) z regulaminem użycia oprogramowania.
I przechodzimy przez dwa ekrany aż do ostatniego, gdzie klikamy Install.
Następnym już etapem będzie uruchomienie oprogramowania i wypełnienie warunków licencji poprzez podanie jaki rodzaj użytkowania nas interesuje – wybieramy wersję Akademicką i uzupełniamy poszczególne pola, zaznaczając, że będziemy używać aplikacji tylko do użytku akademickiego.
Po chwili widzimy już poniższy ekran aplikacji
Sieć Bayesowska – konstrukcja
Przykład: Produkcja chemiczna
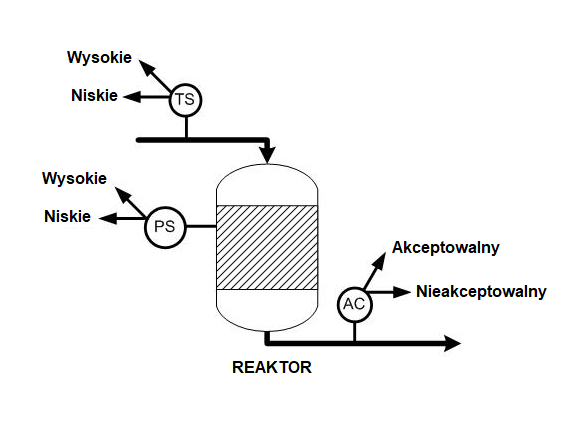
W przypadku reaktora chemicznego pokazanego poniżej prawdopodobieństwo, że strumień odcieku będzie zawierał dopuszczalny ułamek molowy produktu, wynosi 0,5. W przypadku tego samego reaktora, jeśli strumień odcieku zawiera dopuszczalny ułamek molowy, prawdopodobieństwo, że ciśnienie w reaktorze jest wysokie, wynosi 0,7. Jeśli strumień odcieku nie zawiera dopuszczalnej frakcji, prawdopodobieństwo, że ciśnienie jest niskie, wynosi 0,85. Jeśli ciśnienie w reaktorze jest wysokie, prawdopodobieństwo, że temperatura surowca jest wysoka, wynosi 0,9, a jeśli ciśnienie w reaktorze jest niskie, prawdopodobieństwo, że temperatura wsadu jest niska, wynosi 0,75.
Biorąc pod uwagę, że temperatura surowca jest niska, jakie jest prawdopodobieństwo, że strumień ścieków zawiera dopuszczalny ułamek molowy produktu?
Rozwiązanie:
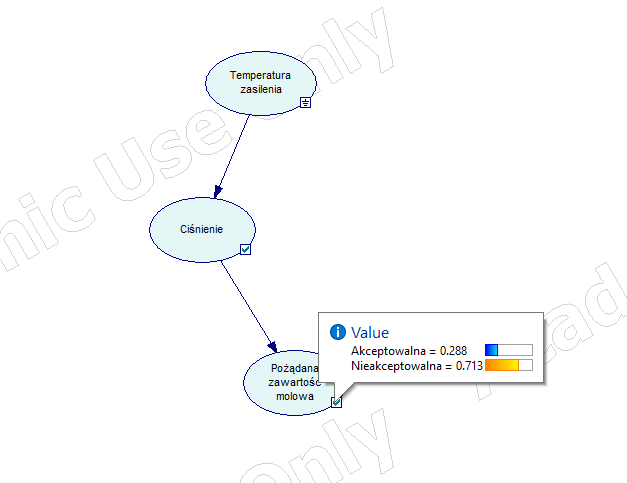
Zmienne, które należy uwzględnić w sieci bayesowskiej, to dopuszczalny ułamek molowy produktu w strumieniu odcieku, ciśnienie w reaktorze i temperatura reaktora. Zmienne są połączone w sieć acykliczną, jak pokazano na poniższym obrazku. Po utworzeniu węzłów i zdefiniowaniu łuków incydentów obliczono prawdopodobieństwo poprzez aktualizację sieci i przesunięcie wskaźnika nad znacznik wyboru na węźle. Jak widać na rysunku, prawdopodobieństwo, że strumień odcieku będzie zawierał dopuszczalny ułamek molowy produktu przy niskiej temperaturze zasilania, wynosi 29%.
Zadania
Zadanie 1: Zaliczyć!
Jakie są szanse zdania ustnego egzaminu u prof. X, który jest kibicem Wisły i nie lubi deszczu? Szansa na awans Wisły to 0.2. Szansa na deszcz to 0.3. Szansa, że student weźmie się do nauki to 0.2. Jeśli Wisła awansuje i nie będzie deszczu, to profesor będzie miał dobry humor na 0.99, jeśli będzie padać to na 0.95. Jeśli jednak Wisła odpadnie, a deszcz będzie padać to szansa na dobry humor to 0.05, jeśli nie będzie padać, to 0.15.
Określając zależności wynika z tego, że humor profesora zależy od dwu czynników, tak samo jak i zaliczenie. Graf Bayesa może wyglądać następująco:
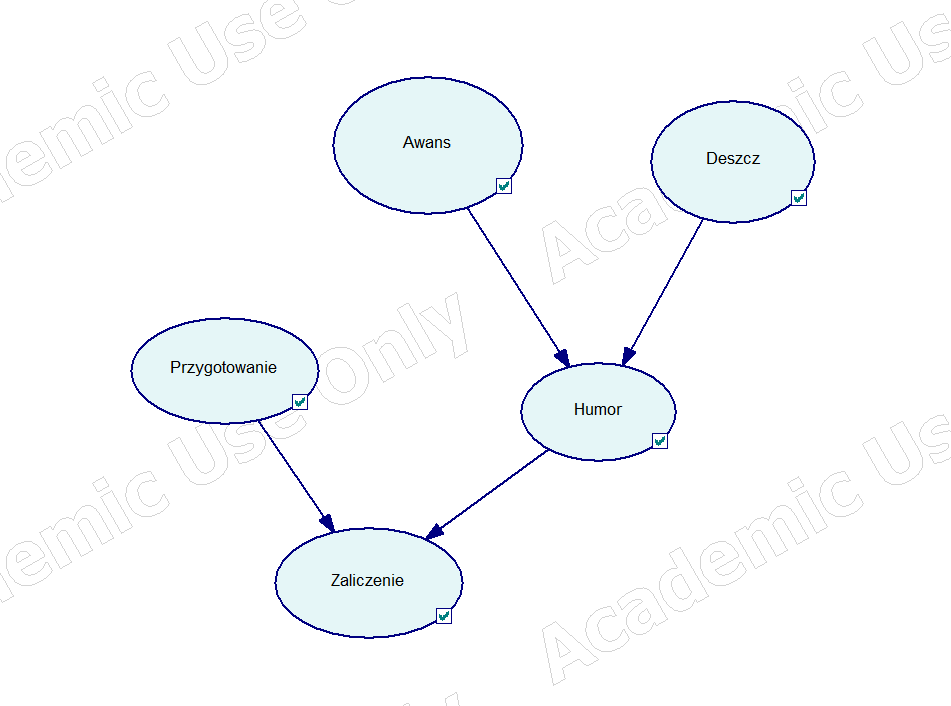
W poszczególne prawdopodobieństwa zostały określone „doświadczalnie” lub „statystycznie”, tak więc prawdopodobieństwa bazowe:
- P(Awans)=0.20
- P(Deszcz)=0.30
- P(Nauki)=0.20
Prawdopodobieństwa zależne:
- P(Humor|Awans,Deszcz)
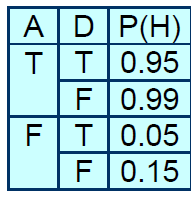
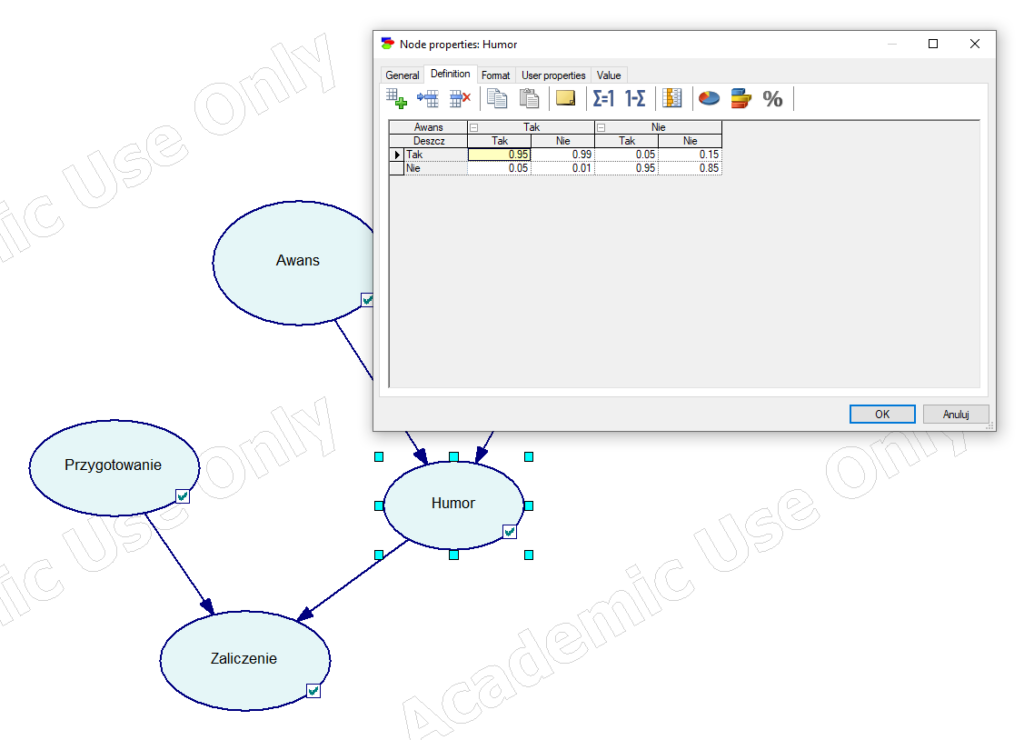
- P(Zaliczenie|Nauka,Humor)
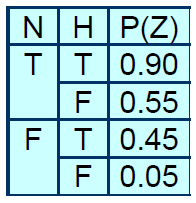
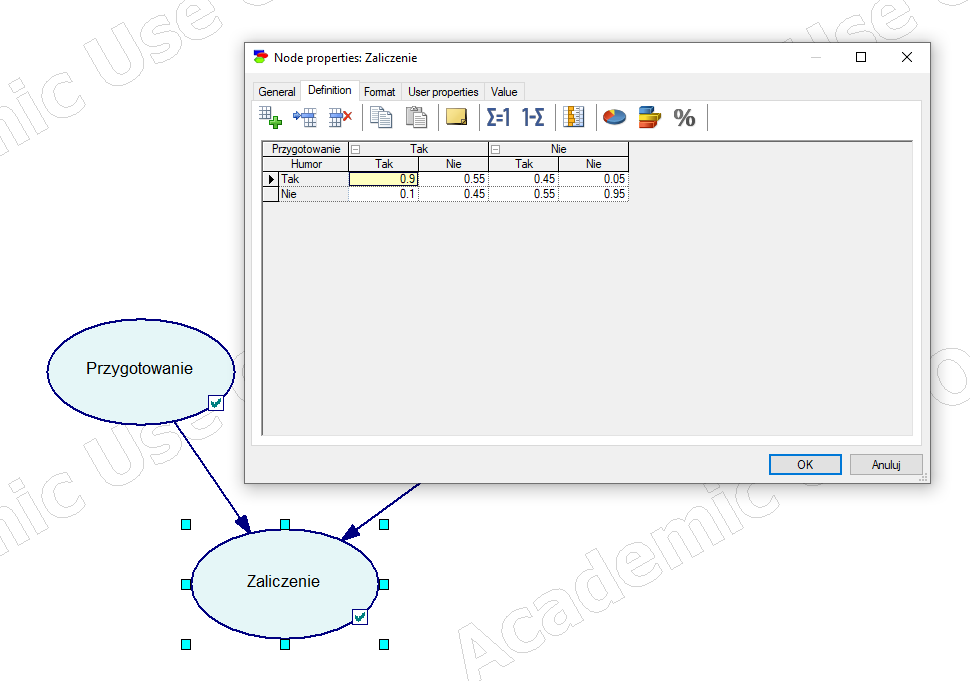
Po ustawieniu tabeli prawdopodobieństw dla każdego węzła możemy pokusić się o przeprowadzenie pierwszych kalkulacji. Aktualizacja sieci (poprzez Update Beliefs z menu sieci, bądź poprzez podwójne kliknięcie „?” na węźle sieci) spowoduje wyliczenie prawdopodobieństw na podstawie wszystkich zależności.
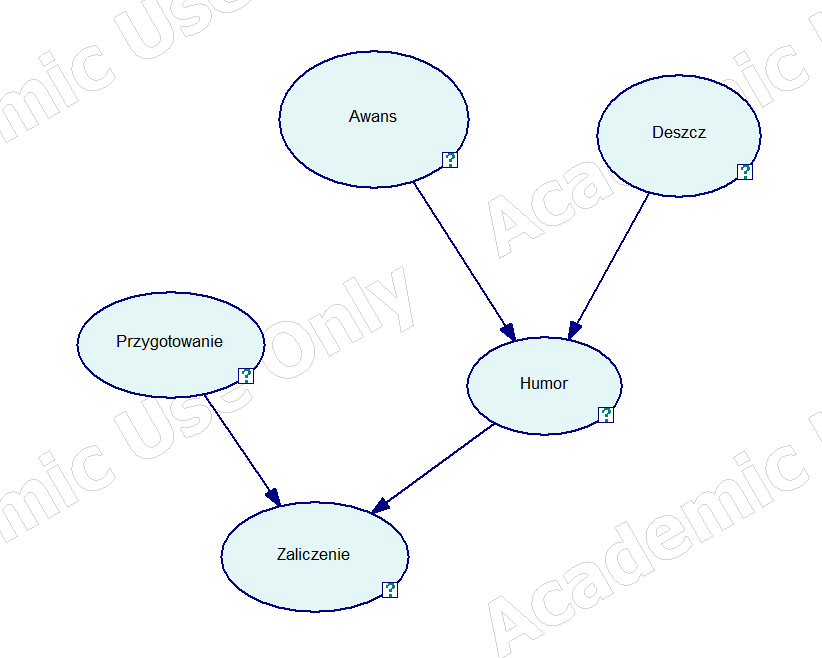
Dla naszego przykładu szansa na zdanie egzaminu to 0.26. Pozwala nam to przeprowadzić różne testy na tak określonej sieci.
Wariant 1
Załóżmy, że Wisła nie awansowała, pada deszcz, i profesor ma zły humor…
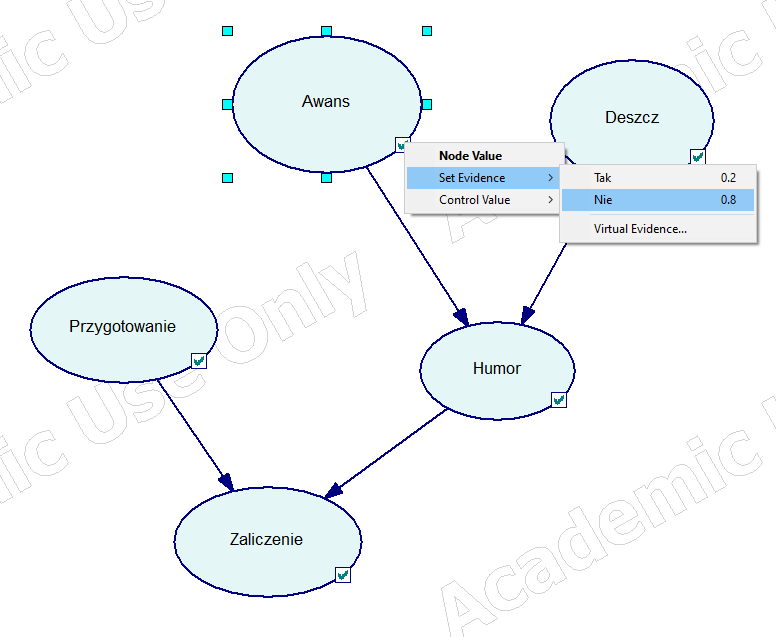
Ustawiamy zatem po kolei wszystkie znane warunki… i otrzymujemy wynik, że prawdopodobieństwo zaliczenia w tych warunkach jest równe 0.05.
Wariant 2
Sprawdźmy co trzeba by zaliczyć. Wobec tego ustawmy parametry egzaminu jako zdany i…
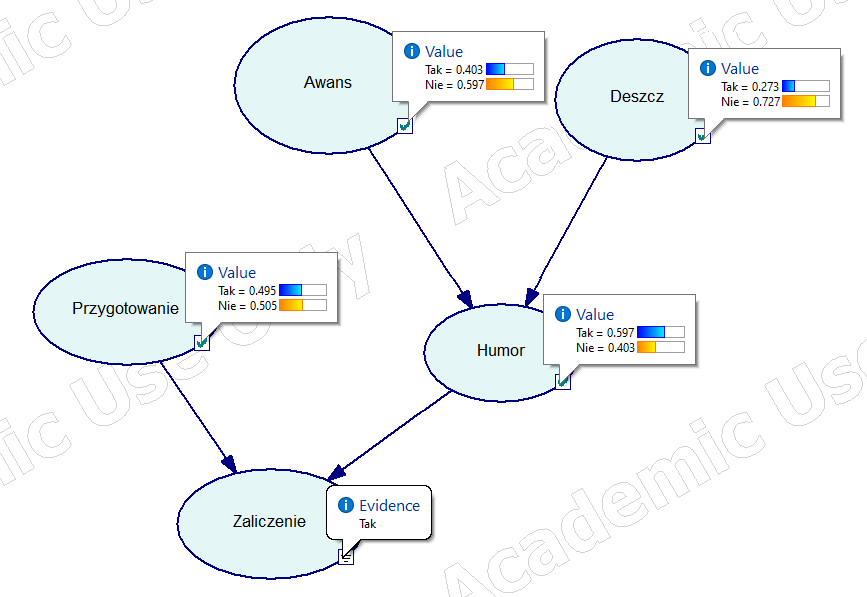
… uzyskujemy konieczne prawdopodobieństwa zaistnienia określonych zdarzeń.
Wariant 3
A co jeśli się przygotujemy na 100%, jak to wpłynie na nasze zaliczenie?! Sprawdź!
A jeśli świeci słońce??
itd.
Zadanie 2: Marketing
Odnieś się do wykładu z Sieci Bayesowskich i analizowanego tam przykładu klasyfikacji osoby o wskazanych cechach do klasy kupujących komputery1slajd 10 i następne. Stwórz sieć bayesowską dla tego przykładu umożliwiając prowadzenie faktoryzacji i diagnostyki. Opis wykonanego zadania w .pdf oraz plik sieci .xdsl wgraj jako rozwiązanie zadania w Moodle.
Zadanie 3: Diagnostyka medyczna
Odnieś się do wykładu z Sieci Bayesowskich i analizowanego tam przykładu diagnostyki medycznej osób podejrzanych o zachorowanie na grypę2slajd 50 i następne. Stwórz sieć bayesowską dla tego przykładu umożliwiając prowadzenie faktoryzacji i diagnostyki. Opis wykonanego zadania w .pdf oraz plik sieci .xdsl wgraj jako rozwiązanie zadania w Moodle.
Zadanie 4: Udany urlop
Obecnie pracuję i spodziewam się, że do dnia w którym wyjadę prawdopodobieństwo, że będę miał pracę wynosi 0.9. Jeśli będę miał pracę, to prawdopodobieństwo zaoszczędzenia na wakacje wynosi 0.75, jeśli nie to może 0.15. Szansa, że szef da mi urlop to 65/35. Gdy wyjadę na urlop to prawdopodobieństwo dobrej pogody w wybranym miejscu jest określone 230 dniami słonecznymi w roku. Jeśli będzie słonecznie to prawdopodobieństwo znaczącej opalenizny wynosi 0.8.
Zakładając, że straciłem pracę jaka jest szansa na zyskanie chociaż opalenizny??