Oprogramowanie umożliwiające tworzenie schematów blokowych to np. Diagram Designer, który jako darmowe narzędzie posłuży nam do zobrazowania algorytmów w postaci schematów (można użyć też narzędzia on-line: draw.io.
W poprzednim temacie omówione zostały podstawowe typy algorytmów. Niniejszy temat traktuje o klasycznych zagadnieniach przedstawianych za pomocą algorytmów.
Spis treści
Całkowity dzielnik
Na początek algorytm sprawdzający czy dana liczba jest podzielna (całkowicie) przez założoną dzielną.
Mamy stworzyć algorytm pobierający od użytkownika dwie liczby, a następnie testujący, czy pierwsza z liczb jest całkowicie podzielna przez drugą. Taki algorytm jest w miarę prosty do stworzenia poprzez analogię do już znanego algorytmu sprawdzającego czy liczba jest parzystą. Można założyć, że jeśli mamy operację dzielenia całkowitego, to istnieje też operacja określająca resztę z dzielenia. Taką operacją matematyczną jest mod. Tak więc:
3 mod 2 = 1
8 mod 3 = 2
10 mod 5 = 0
10 mod 2 = 0
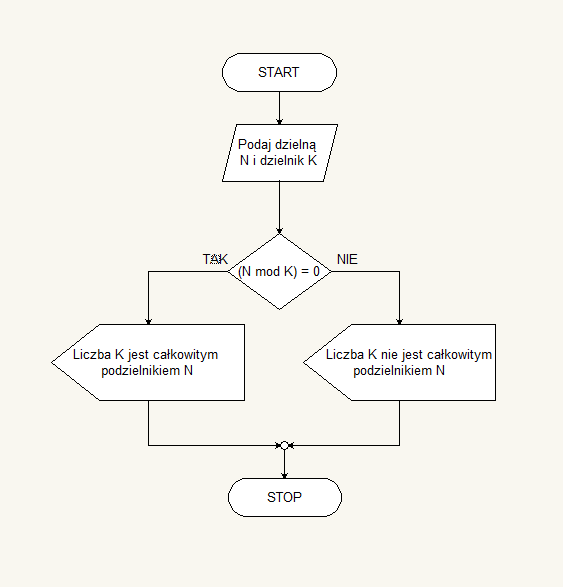
Powyższy przykład po ustaleniu w działaniu algorytmu liczb N i K przystępuje do testu, czy operacja N mod K da w wyniku 0. Wartość 0 jest otrzymywana tylko w przypadku, gdy wielokrotność dzielnika mieści się całkowicie i zupełnie (bez reszty) w dzielnej. Stąd wniosek, że jeżeli wynikiem jest 0 to liczba K jest całkowitym dzielnikiem liczby N.
Spróbuj stworzyć inny algorytm realizujący tę samą funkcjonalność. Nawet jeśli inność polegałaby tylko na innym rodzaju teście (warunku). A może masz pomysł na całkowicie inny algorytm?
Która większa?!
Algorytm sprawdzający, która z podanych liczb jest większa od drugiej? Podnieś rękawicę i opracuj takowy.
Wartość bezwzględna liczby
Stwórz algorytm, który przekształca podaną liczbę rzeczywistą (x ∈ R) w jej wartość bezwzględną.
Trójkąt – czy da się zbudować?!
Algorytm sprawdzający czy z podanych długości boków a, b, c da się zbudować trójkąt. Dasz radę stworzyć algorytm?
Trójkąt – czy prostokątny?!
Rozszerz poprzedni algorytm o test, czy trójkąt zbudowany z boków a, b, c jest trójkątem prostokątnym.
Trójkąt – jakie pole?!
Spróbuj stworzyć algorytm obliczający pole trójkąta na podstawie posiadanych długości jego boków a, b, c (wzór Herona).
Multiplicity
Ile razy mieści się jedna liczba w drugiej?! To zagadnienie na kolejny schemat blokowy. Spróbujesz go zrobić?
Największy wspólny podzielnik NWP
Największym wspólnym podzielnikiem jest taka liczba, która całkowicie dzieli obie testowane liczby i jest największa z całego zbioru wspólnych podzielników.
Silnia
Algorytm obliczania n!, gdzie n ∈ N. Zmierz się z nim.
Liczba pierwsza
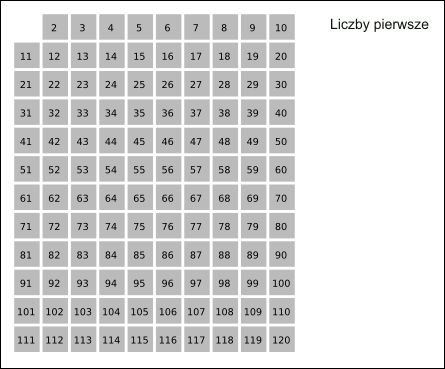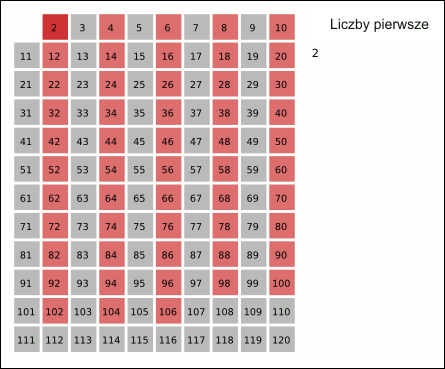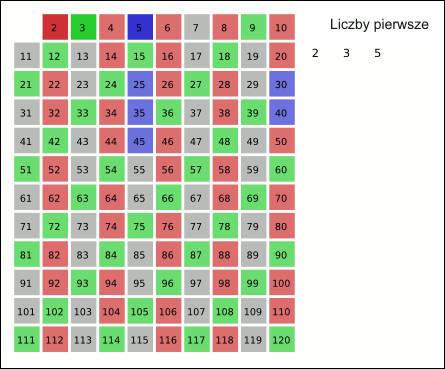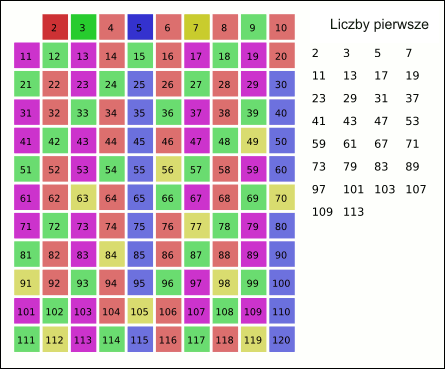
Liczba pierwsza to liczba naturalna (k ∈ N) większa od 1, która ma dokładnie dwa dzielniki naturalne: jedynkę i siebie samą. Jest kilka algorytmów szukania liczb pierwszych. Spróbujesz sam wymyślić sposób jak sprawdzić, czy liczba k jest liczbą pierwszą?
Potęgowanie (nie rekurencyjne)
W poprzednim temacie został użyty algorytm potęgowania xy z wykorzystaniem rekurencji. Nie jest to jednakże jedyny sposób na potęgowanie. Spróbuj zastanowić się nad innym.
Zadania do samodzielnego wykonania: Podane wyżej zadania należy opracować w Diagram Designer’ze, a wyniki w postaci raportu PDF z 11 schematami blokowymi oraz opisem krok po kroku ich działania ww. algorytmów załączyć w Moodle.